How many bags are you going to need?

It depends on how much fill you put in your bags, and what size bags you choose. We'll discuss options further down the page.

Quick answer: Let's assume you're using standard 14"x26" bags and filling them about 2/3 way (approx. 40 lbs) as in the table to the left. These will give you tamped (finished) dimensions of approximately 15" (1.25 foot) long,12" wide and 3" high.

Multiply your intended wall's width by its height; the total gives you the square footage of that one wall. Refer to the table on the left. A wall 15' wide x 8' high would be 120 square feet. The table indicates you'd need about 500 bags.

How it works (alternate method):

1.) Measure the linear width of one of your walls. Each foot & a quarter (15") = 1 bag. A 15 foot-wide wall, divided by 1.25 (the length of a filled & tamped bag) would require about 12 bags butted end-to-end per course.

2.) A 40 lb bag will be about 3" high after tamping, making each course 3" high. Every 4 courses will amount to one vertical foot. If your wall is 8 feet high, you'll need 32 courses.

Using this method, the above-described 15'W x 8'H wall will require about 12 bags per course & about 32 courses for a total of 384 bags, which is close to the first method.

Figure out the dimensions of your remaining 3 walls, subtract for your doors & windows & you'll have a rough idea of the total number of bags your structure will need.

Heavier bags: Some folks like to fill their 14" x 26" bags to as much as 60 lbs each. These will have tamped dimensions of approximately:

• 18" (1.5 feet) long,
• 12" wide, and
• 4-6" high.

Take note that, at 4" high, you'll only need 3 courses per vertical foot.

The obvious advantage of heavier bags is that you will need fewer bags. The disadvantage is that they're much harder to handle, especially as your walls rise and you're lifting them up over your head to place them.

Lighter bags = more bags = less labor.
Heavier bags = fewer bags = more labor.

Using these tables, you can estimate the number of 60 lb bags you'll need by halving the bag count in the column to the left. The same 15' W x 8" H wall mentioned above would require 10 bags per course (at 18" long) and only 24 courses, for a total of about 240 bags.

In all cases, regardless of how much fill you put in them, 14"x26" bags will pretty much remain 12" wide (meaning your walls will be about a foot thick, before plastering),

We carry larger bags (18"x30" but at 75-90 lbs each, they're pretty hard for most people to handle.

Consistency: It'll be to your advantage to fill your bags as consistently as possible to keep your courses straight & to streamline your production with assembly-line precision (see our Techniques page). Sure, you can be organic and free-form (eyeballing the filled bag, guessing at the weight), but you risk introducing small errors that can grow exponentially, and you also risk work slowdowns caused by futzing around.

Calculating how many bags you'll need for something like a wall is to simply figure how many square feet the face of the construction will be (H x L). A very basic rule of thumb is 4:1 - four bags for every square foot.

Take, for example, a wall 5 feet high by 10 feet long. Your area would be 5' x 10' = 50 sq. feet.

Taking this figure, you can do one of 3 things:

• Use the 4:1 guideline (four bags for every square foot). Fifty times four = 200.


• Use the chart to the left as a guide (which uses our dimensions of 12" x 12" x 3"). Looking up 50 sq. feet in the 3rd column shows that you'd need 200 bags. 


• Divide your square footage by 0.33 square feet, which is arrived at by calculating the side profile of a 12"L x 3"H bag. (50 / 0.25 = 200 bags).

If you're considering building something curved or circular,  then calculating how many 12" long filled bags you'll need will start with this formula:

d * pi  = number of bags

where d=diameter and pi = 3.14. Multiplying these will give you your circumference. Since 30 pound bags are 1 ft long, this figure will give you your approximate per-course bag count. (A "course" = a single horizontal row.) If you're using 60 lb. bags (18" long or 1.5 feet long), then you'll need to divide your circumference by 1.5 to arrive at the number of bags needed.

A 10-foot diameter round structure will have a circumference of 31.4 feet. You'll need 31.4 thirty-pound bags. For 60-pound bags, you'll need to divide 31.4 by 1.5 to arrive at 20.9 (21) filled bags per course.

As to height: if your tamped bags are 3" high, you'll need four courses for one vertical foot of wall height. So 8 foot high walls, will require 32 courses of 31.4 bags per course = 1005 bags. (Fewer bags, of course, if you're planning on having doors or windows.) 60-pound bags (4" high, 3 courses per vertical foot) will require 24 courses, so 24 x 21 = 504 bags.

Establish whether your diameter is inner or outer; it'll make a difference, considering that your walls are about 14" thick after plastering.

You can lay out & control your circles & arcs by driving a pin or pole in the center of your building site, and then using either string or a lightweight pole as a pivoting compass.

Again, if you're filling your own bags to different dimensions (or using different sized bags), you may have to make corresponding changes to the  formulas provided.

---

Arcs and sectors

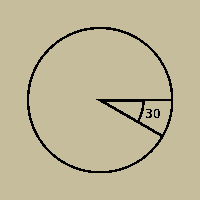
It also might be helpful to know how to calculate the arc or sector of a circle. An arc is a segment of the circumference - you'd use this to, say, figure the width of a doorway or a window. A sector is a pie-shaped chunk of the circle starting at the center and going out to the circumference. It can be defined by its angle.

By determining the length of your arc in feet, you can get an idea of how many bags you'll need - or (in the case of a doorway) how many bags you won't need. Here's a formula:


where x is the degree of your sector, d=the diameter of your circle and pi = 3.14. Multiply these together. 60 lb bags? Divide by 1.5.

Example 1: You have a structure with a diameter of 10 feet and (see above) a circumference of 31.4 feet, requiring a total of 31.4 thirty-lb. bags. You know the angle of your sector is 30 degrees (x). So pi * 10 * 30 = 942. Divide this by 360 and you have 2.6 feet (the length of your arc - or, more practically, the width of your dome's door or window). Subtract 2.6 bags (the door) from 31.4 bags (the total needed) and you arrive at 28.8 bags for each course where there'll be a gap for the doorway. Do this for all your doors & windows when calculating how many bags you can subtract from the total bags you'll be needing.

 Example 2: A quarter-circle retaining wall (say, a flower bed in the corner of your yard) has a sector of 90 degrees and a radius of six feet. Your full circle would have a diameter of 12 feet; 12 * pi would give you a circumference of  37.68 feet. Divide this by four (remember, it's a quarter circle) and you have an arc of 9.42 feet. Your courses will require 9.42 (say, 9.5) end-to-end 30 lb. bags, or (for sixty-lb bags, dividing by 1.5), 6.28 bags.

Play with this. You'll get the hang of it. Or you can email us at info@nmdirtbags and we'll see if we can help.

---

Why include the weight?

Bag weight is included for several reasons, not the least to give you food for thought regarding the importance of preparing your foundation. Without a good foundation, differential settling and compaction of the ground can cause everything from minor to catastrophic problems with your structure. The critical importance of understanding this, of establishing a good foundation, and of maintaining a high degree of quality control as your walls rise cannot be overstated.

Gravity exerts its force straight downwards. The sheer weight of the bags pressing straight down over time can help consolidate your project's structural integrity... if your foundation is rock-solid, and if you carefully maintain vertical walls with a level and/or a plumb bob. Click here for illustration.

If a 10 foot long, 8 foot high wall (weighing some 9,000 lbs) is not perfectly vertical - that is to say, if the mass is being directed downward at an angle - then the resulting instability can "creep" over time and result in cracking plaster, sticking doors, or - worst case - total structural collapse. 

Conversely, if you're building a dome or an arch (doorway, window), then you'll want to offset or stagger your bags to direct the weight/mass to your needs. It's not our scope here to describe this here. We highly recommend Kaki Hunter & Donald Kiffmeyer's indispensible Earthbag Building.

---

If you're considering building a habitation, it's mandatory here in New Mexico to enlist the services an architect or a structural engineer to sign off on your plans. Elsewhere, it's still  a good idea. Doing so will not only ensure peace of mind, but may be an important or essential factor in securing a building permit and home insurance.

We hope to be posting more on this site on the how-to's of building structures & relevant codes.

---